18 непрерывность дифференцируемой функции имеющих производную. Дифференцируемость функций. непрерывность дифференцируемой функции. Геометрический смысл производной

Пусть функция у = f{x) определена на интервале (а, 6). Возьмем некоторое значение х € {а, Ь). Дадим х приращение Дя любое, но такое, чтобы х + Дя € (а, 6). Тогда функция у = f(x) получит прирашение Определение. Функция у = f(x) называется дифференцируемой в точке х £ (а, 6), если прирашение функции отвечающее прирашению Ах аргумента, можно представить в виде где А - некоторое число, которое не зависит от Ах (но, вообше говоря, зависит Пример. Рассмотрим функцию у = х2. Во всякой то»«е х и при любом Дх имеем Отсюда, в силу определения, функция у = х2 дифференцируема в любой точке х, причем Следующая теорема выражает необходимое и достаточное условие дифференци-руемости функции. Теорема 1. Для того чтобы функция у = fix) была дифференцируемой в точке х, необходимо и достаточно, чтобы fix) в этой точке имела конечную производную f\x). Необходимость. Пусть функция у = fix) дифференцируема в точке х. Докажем, что в этой точке существует производная fix). Действительно, из дифференцируемости функции у = fix) в точке х следует, что приращение функции Ду, отвечающее приращению Дх аргумента, можно представить в виде Дифференцируемость функции. Дифференциал функции Непрерывность дифференцируемой функции Понятие дифференциала функции Геометрический смысл дифференциала где величина А для данной точки х постоянна (не зависит от. По теореме о связи функции, имеющей предел, с ее пределом и бесконечно малой функцией, отсюда следует, что Существование производной доказано. Одновременно мы установили, что Достаточность. Пусть функция в точке х имеет конечную производную /"(х). Докажем, что fix) в этой точке дифференцируема. Действительно, существование производной /"(х) означает, что при Дх 0 существует предел отношения и что Отсюда, в силу теоремы о связи функции, имеющей предел, с ее пределом и бесконечно малой функцией, вытекает, что где, значит, Так как в правой части формулы (2) величина х) не зависит от, то равенство (2) доказывает, что функция у = /(х) дифференцируема в точке Теорема 1 устанавливает, что для функции /(х) дифференцируемостьв данной точке х и сушествованйе конечной производной в этой точке - понятия равносильные. Поэтому операцию нахождения производной функции называют также дифференцированием этой функции. В дальнейшем, когда мы говорим, что функция /(х) имеет производную в данной точке, мы подразумеваем наличие конечной производной, если не оговорено противное. 2.1. Непрерывность дифференцируемой функции Теорема 2. Если функция дифференцируема в данной точке х, то она непрерывна в этой точке. Действительно, если функция у = /(х) дифференцируема в точке х, то приращение Ду этой функции, отвечающее приращению Дх аргумента, может быть представлено в виде где А - постоянная для данной точки х, а а 0 при Дх 0. Из равенства (3) следует, что Дифференцируемость функции. Дифференциал функции Непрерывность дифференцируемой функции Понятие дифференциала функции Геометрический смысл дифференциала что и означает, согласно определению, непрерывность функции у = /(х) в данной точке х. Обратное заключение неверно: из непрерывности функции /(х) в некоторой точке х не следует дифференцируемость функции в этой точке. Пример. Например, функция /(х) = |х| непрерывна в точке х = 0, но, как мы показали выше (, не имеет производной в точке х = 0 и потому не является дифференцируемой в этой точке. Приведем еше пример. Пример. Функция непрерывна на интервале (-о#, +о#). Для всех х # 0 она имеет производную, но в точке х = 0 она не имеет ни правой, ни левой производной, потому что величина не имеет предела, как при В приведенных примерах производная отсутствует лишь в одной точке. Так и думали в XVIII и начале XIX в., когда считали, что непрерывная функция может не иметь производной самое большее в конечном числеточек. Позжебыли построены (Больца-но, Вейерштрасс, Пеано, Ван дер Варден) примеры непрерывных на отрезке [а, Ь\ функций, не имеющих производной ни в одной точке отрезка. Понятие дифференциала функции Пусть функция у - /(х) дифференцируема в точке х, т.е. прирашение Ду этой функции, отвечающее приращению Дх аргумента, представимо в виде Определение. Если функция у = f(x) дифференцируема в точке х, точасть приращения функции А Дх при Аф 0 называется дифференциаюм функции у = /(х) и обозначается символом dy или df{x): В случае А Ф 0 дифференциал функции называют главной линейной частью приращения Ду функции, поскольку при Дх 0 величина а(Дх)Дх в равенстве (4) есть бесконечно малая функция более высокого порядка, чем А Дх. В случае, когда >1 = 0, считают, что дифференциал dy равен нулю. В силу теоремы I имеем А = /"(х), так что формула (5) для dy принимает вид. Наряду с понятием дифференциала функции вводят понятие дифференциала dx независимой переменной х, полагая по определению Тогда формулу для дифференциала функции у = /(х) можно записать в более симметричной форме Отсюда в свою очередь имеем: /"(х) = Это еще одно обозначение производной (iобозначение Лейбница), которую можно рассматривать как дробь - отношение дифференциала функции dy к дифференциалу аргумента dx. Введем еше одно понятие. Будем говорить, что функция у = /(х) дифференцируема на интервале (а, Ь), если она дифференцируема в каждой точке этого интервала. Дифференцируемость функции. Дифференциал функции Непрерывность дифференцируемой функции Понятие дифференциала функции Геометрический смысл дифференциала Геометрический смысл дифференциала Пусть имеем кривую, заданную уравнением у = /(х),гдс /(х) - дифференцируемая в точке х € (а, 6). Проведем касательную к этой кривой в точке М(х,у) и отметим на кривой еще точку М\ с абсциссой х -f dx. Как известно, /"(х) есть угловой коэффициент касательной, т.е. Рассмотрим треугольник MPQ (рис.8). Из рисунка видно, что Таким образом, дифференциал dy = f"(x)dx функции у = f(x) есть приращение ординаты касательной, проведенной к кривой у = f(x) в точке с абсциссой ж, при переходе от точки касания к точке с абсциссой х + dx.

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

Доказательство . Если, то

где б бесконечно малая величина, т.е. величина, стремящаяся к нулю при Дx>0. Но тогда

Дy=f "(x 0) Дx+бДx=> Дy>0 при Дx>0, т.е f(x) - f(x 0)>0 при x>x 0 ,

а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Дx>0 отношение не имеет предела (т.к. односторонние пределы различны при Дx>0-0 и Дx>0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Дx>0 отношение является знакопостоянной бесконечно большой величиной. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки - "точка перегиба" c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип - "точка возврата" с вертикальной касательной - частный случай угловой точки.

1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке

Покажем, что она не имеет производной в этой точке.

f(0+Дx) = f(Дx) = |Дx|. Следовательно, Дy = f(Дx) - f(0) = |Дx|

Но тогда при Дx< 0 (т.е. при Дx стремящемся к 0 слева)

А при Дx > 0

Т.о., отношение при Дx> 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Функция y = f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а ; b ] или интервала (а ; b ), то говорят, что она дифференцируема на отрезке [а ; b ] или соответственно в интервале (а ; b ).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y = f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

Доказательство . Если , то

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx →0. Но тогда

Δy =f "(x 0 ) Δx +αΔx => Δy →0 при Δx →0, т.е f(x) - f(x 0) →0 при x →x 0 , а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx →0 отношение не имеет предела (т.к. односторонние пределы различны при Δx →0-0 и Δx →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Δx →0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки - "точка перегиба" c вертикальной касательной.

Примеры.

1. Рассмотрим функцию y=|x| . Эта функция непрерывна в точке x = 0, т.к. .

Покажем, что она не имеет производной в этой точке.

f (0+Δx ) = f (Δx ) = |Δx |. Следовательно, Δy = f (Δx ) - f (0) = |Δx |

Но тогда при Δx < 0 (т.е. при Δx стремящемся к 0 слева)

А при Δx > 0

Т.о., отношение при Δx → 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x | в точке x = 0 не существует. Геометрически это значит, что в точке x = 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x = 0.

Следовательно, рассматриваемая функция не дифференцируема в точке x = 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy .

Производные элементарных функций.

1.
y = x n . Если n - целое положительное число, то, используя формулу бинома Ньютона:

(a + b ) n = a n +n·a n-1 ·b + 1/2?n(n - 1)a n-2 ?b 2 + 1/(2?3)?n(n - 1)(n - 2)a n-3 b 3 +…+ b n ,

можно доказать, что

Итак, если x получает приращение Δx , то f(x +Δx) = (x + Δx) n , и, следовательно,

Формулы 3 и 5 докажите самостоятельно.

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a , b ], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b , непрерывна соответственно справа и слева.

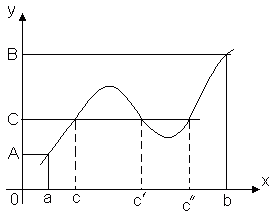
Теорема 1. Функция, непрерывная на отрезке [a , b ], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a , b ], то найдётся хотя бы одна точка x 1 Î [a , b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x 1) ≥ f(x) . Аналогично найдётся такая точка x 2 , в которой значение функции будет самым маленьким из всех значений на отрезке: f(x 1) ≤ f(x) .

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x 2 и x 2 ".

Замечание . Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a , b ). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a , b ], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a , b ] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка найдется, по крайней мере, одна точка x = C , в которой функция обращается в ноль: f(C) = 0, где a < C< b

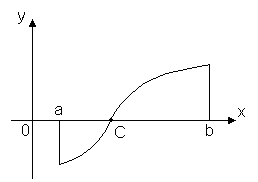
Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x) , соответствующие концам отрезка [a , b ] лежат по разные стороны от оси Ox , то этот график хотя бы в одной точке отрезка пересекает ось Ox . Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a , b ] и f(a) = A , f(b) = B . Тогда для любого числа C , заключённого между A и B , найдётся внутри этого отрезка такая точка C Î [a , b ], что f(c) = C .

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x) . Пусть f(a) = A , f(b) = B . Тогда любая прямая y = C , где C – любое число, заключённое между A и B , пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C , при котором f(c) = C .

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x 0 и новое x .

Разность x– x 0 называется приращением аргумента x в точке x 0 и обозначается Δx . Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx , т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx) .

Разность y – y 0 = f(x) – f(x 0 ) называется приращением функции y = f(x) в точке x 0 и обозначается символом Δy . Таким образом,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Обычно исходное значение аргумента x 0 считается фиксированным, а новое значение x – переменным. Тогда y 0 = f(x 0 ) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δx также будут переменными и формула (1) показывает, что Dy является функцией переменной Δx .

Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x 0 и обозначают f "(x 0). Итак,

Производной данной функции y = f(x) в точке x 0 называется предел отношения приращения функции Δy к приращению аргумента Δx , когда последнее произвольным образом стремится к нулю.

Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x . Эта функция обозначается f "(x )

Производная обозначается символами f "(x),y ", . Конкретное значение производной при x = a обозначается f "(a ) или y "| x=a .

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило :

Примеры.

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t , где s – путь, пройденный к моменту времени t , v – скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние s будет зависеть от времени t , т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t 0 . К этому моменту точка прошла путь s=s(t 0 ). Определим скорость v материальной точки в момент времени t 0 .

Для этого рассмотрим какой-нибудь другой момент времени t 0 + Δt . Ему соответствует пройденный путь s=s(t 0 + Δt ). Тогда за промежуток времени Δt точка прошла путь Δs=s(t 0 + Δt) –s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt . Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t 0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt .

Итак, скоростью движения в данный момент времени t 0 (мгновенной скоростью) называется предел средней скорости в промежутке от t 0 до t 0 +Δt , когда Δt →0:

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М 0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M 0 M . Если точка М начинает перемещаться по кривой, а точка М 0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М 0 с любой стороны секущая стремится занять положение определенной прямой М 0 Т , то прямая М 0 Т называется касательной к кривой в данной точке М 0 .

Т.о., касательной к кривой в данной точке М 0 называется предельное положение секущей М 0 М , когда точка М стремится вдоль кривой к точке М 0 .

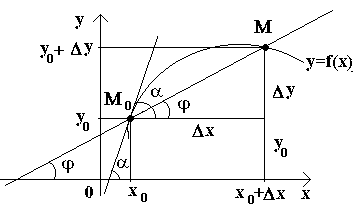
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х 0 функция принимает значение y 0 =f(x 0). Этим значениям x 0 и y 0 на кривой соответствует точка М 0 (x 0 ; y 0). Дадим аргументу x 0 приращение Δх . Новому значению аргумента соответствует наращенное значение функции y 0 +Δ y=f(x 0 –Δx) . Получаем точку М(x 0 +Δx ; y 0 +Δy). Проведем секущую М 0 М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox . Составим отношение и заметим, что .

Если теперь Δx →0, то в силу непрерывности функции Δу →0, и поэтому точка М , перемещаясь по кривой, неограниченно приближается к точке М 0 . Тогда секущая М 0 М будет стремиться занять положение касательной к кривой в точке М 0 , а угол φ→α при Δx →0, где через α обозначили угол между касательной и положительным направлением оси Ox . Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

т.е. f "(x) = tg α .

Т.о., геометрически у "(x 0) представляет угловой коэффициент касательной к графику этой функции в точке x 0 , т.е. при данном значении аргумента x , производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М 0 (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М (-1; 1).

Ранее мы уже видели, что (x 2)" = 2х . Но угловой коэффициент касательной к кривой есть tg α = y "| x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство . Если , то

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx →0. Но тогда

Δy =f "(x 0 ) Δx +αΔx => Δy →0 при Δx →0, т.е f(x) – f(x 0) →0 при x →x 0 , а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx →0 отношение не имеет предела (т.к. односторонние пределы различны при Δx →0–0 и Δx →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Δx →0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.

Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–< х < ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

21 Правила нахожд. производ. суммы

Правило 1. Если функции у = f(х) и у = g(х) имеют, производную в точке х, то и их сумма имеет производную в точке х, причем производная суммы равна сумме производных:
(f(х) + 8(х))" =f (х)+ (х).
На практике это правило формулируют короче: производная суммы равна сумме производных.
Например,
Правило 2. Если функция у = f(х) имеет, производную в точке х, то и функция у = кf(х) имеет производную в точке х, причем:

На практике это правило формулируют короче: постоянный множитель можно вынести за знак производной. Например,

Правило 3. Если функции у=f(х) и у =g(х) имеют производную в точке х, то и их произведение имеет производную в точке х, причем:

На практике это правило формулируют так: производная произведения двух функций равна сумме двух слагаемых. Первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Например:
Правило 4. Если функции у = f(x) и у=g(х) имеют производную в то и частное имеет производную в точке х, причем:

Таблица сложных производных

22 Диффир. функц. в точке

Функция y =f (x ) называется дифференцируемой в точке x 0, если ее приращение Δy (x 0,Δx ) может быть представлено в виде

Δy (x 0,Δx )=A Δx +o (Δx ).

Главная линейная часть A Δx приращения Δy называется дифференциалом этой функции в точке x 0, соответствующим приращению Δx , и обозначается символом dy (x 0,Δx ).

Для того, чтобы функция y =f (x ) была дифференцируема в точке x 0, необходимо и достаточно, чтобы существовала производная f ′(x 0), при этом справедливо равенство A =f ′(x 0).

Выражение для дифференциала имеет вид

dy (x 0,dx )=f ′(x 0)dx ,

где dx =Δx .

23 Производ. Слож. Функц

Производная сложной функции. Производная функции, заданной параметрически

Пусть y – сложная функция x , т.е. y = f (u ), u = g (x ), или

Если g (x ) и f (u ) – дифференцируемые функции своих аргументов соответственно в точках x и u = g (x ), то сложная функция также дифференцируема в точке x и находится по формуле

Производная функции заданной параметрически.

24 Произв и диффер. Высш.порядк

Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда

Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Дифференциалом порядка n , где n > 1 , от функции в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n - 1) , то есть

Для функции, зависящей от одной переменной второй и третий дифференциалы выглядят так:

Отсюда можно вывести общий вид дифференциала n -го порядка от функции :

25 Теоремы Ферма, Ролля, Лангража

v Теорема Ферма: Пусть функция определена на и достигает своего наибольшего и наименьшего значения (M и m ) в некоторой из . Если существует производная в , то она обязательно равна 0.

Доказательство: Существует . Возможны два случая:

1) , => , => .

2) , => , => .

Из 1) и 2) следует, что

v Теорема Ролля (о корнях производной): Пусть функция непрерывна на и дифференцируема на и на концах отрезка принимает одинаковые значения: . Тогда существует хотя бы одна точка из , производная в которой .

v Доказательство: Непрерывная достигает на M и m . Тогда возможны два случая:

2) наибольшее значение достигается внутри интервала по теореме Ферма.

v Теорема Лангража (о конечных приращениях): Пусть функция непрерывна на и дифференцируема на . Тогда существует хотя бы одна из , для которой выполняется следующее равенство: .

Доказательство: Введем функцию . (непрерывная на и дифференцируемая на ).

Функция удовлетворяет Теореме Ролля существует , для которой: , , , .

· функция называется стро́го возраста́ющей на , если

· функция называется убыва́ющей на , если

· функция называется стро́го убыва́ющей на , если